Base y Dimensión de Un Espacio Vectorial, [PPTX Powerpoint]

El vector (0,0) solamente puede generar el espacio { (0,0)}, se lo llama subespacio trivial. El vector (1,-1) puede generar un subespacio no trivial (que no sea el { (0,0)}, llamémoslo S. El subespacio que genera (1,-1) es el conjunto de elementos que resultan ser una combinación lineal, aunque en este caso solamente múltiplos, de este vector.
Conjunto Generador de un Espacio Vectorial YouTube

Introducción. En esta entrada explicaremos cómo podemos estudiar espacios y subespacios vectoriales a partir de conjuntos más pequeños que guardan la información más relevante de ellos. A estos conjuntos les llamaremos generadores.Además estudiaremos el concepto de independencia lineal.A grandes rasgos podemos decir que un conjunto es linealmente independiente cuando no tiene.
Espacios Vectoriales Demostrar que R2 es un espacio vectorial Ejercicio resuelto YouTube

INTRODUCCIÓN Llegamos a la conclusión de que la base de un espacio vectorial (con dimensión finita) es un conjunto lo «suficientemente grande» para generar al espacio y lo «suficientemente pequeño» para seguir siendo linealmente independiente. Ahora bien, veremos que siempre será posible encontrar un base si conocemos un conjunto generador finito o un conjunto linealmente […]
Espacio Vectorial Con Producto Interno PDF Ortogonalidad Base (álgebra lineal)

Espacios vectoriales generados y ejemplos de independencia lineal.. por los otros dos vectores que al final si tenemos dos vectores que son en linealmente independientes entonces su espacio el generador es un plano te acuerdas que eso lo vimos en los vídeos pasados por lo tanto este tercer vector tendría que existir en ese plano y por lo.
Vectores generadores o conjunto generador de un espacio vectorial Ejemplo 2 Millermatematcas

3.1. Sistemas de generadores. Definición 3.1. conjunto generador. 18 CÉSAR ROSALES GEOMETRÍA I. 3. Bases, dimensión y coordenadas en un espacio vectorial Una de las ideas principales en la teoría de espacios vectoriales consiste en expresar todos los vectores a partir de unos cuantos mediante combinaciones lineales.
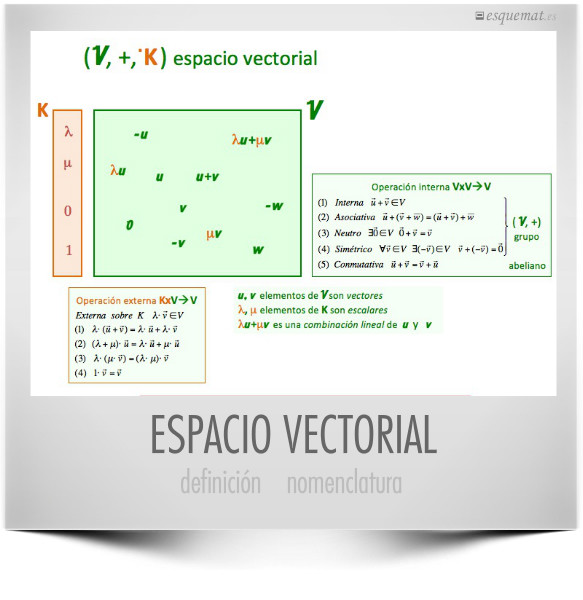
espacio vectorial Esquemat
Definición. Sean v 1,., v n vectores en un espacio vectorial V sobre F. v = c 1 v 1 + c 2 v 2 + ⋯ + c n v n. El espacio generado (que a veces abreviaremos como el generado) por v 1,., v n es el subconjunto de V de todas las combinaciones lineales de v 1,., v n, y lo denotamos por span ( v 1,., v n). Ejemplo.
DETERMINE si el conjunto dado de VECTORES GENERA el espacio VECTORIAL Combinación Lineal YouTube

Clases, SOLUCIÓN ejercicios, trabajos, EXÁMENES resueltos https://linktr.ee/profe_javiCapítulos 0:59 definición de conjunto generador 4:07 combinación lineal.
🧐¿Es un espacio vectorial? Los axiomas o reglas Introducción Álgebra Lineal 3 ejemplos

Encuentra las bases de un espacio vectorial paso a paso. La calculadora encontrará una base del espacio abarcado por el conjunto de vectores dados, con los pasos que se muestran. Calculadoras relacionadas: Calculadora de independencia lineal, Calculadora de rango de matriz. Número de vectores: Tamaño de los vectores: Vectores:
Conjunto Generador De Un Espacio Vectorial Algebra Lineal Otosection

Una base de un espacio vectorial es un sistema generador cuyos vectores son linealmente independientes. Todas las bases de un mismo espacio vectorial tienen el mismo número de vectores y ese número se llama dimensión del espacio vectorial. Todo espacio vectorial tiene, al menos, una base, y cualquier vector se puede expresar de forma única.
Espacio Vectorial Ejercicios Base (Cálculo 3) YouTube

Una base de un espacio vectorial es un sistema generador, cuyos vectores son linealmente independientes. Todas las bases de un mismo espacio vectorial tienen el mismo número de vectores y ese número se llama dimensión del espacio vectorial. Todo espacio vectorial tiene, al menos, una base, y cualquier vector se puede expresar de forma única.
Dimensión de un Espacio Vectorial Definición y Resultados Básicos Álgebra Lineal 6 YouTube

En álgebra lineal, dado un espacio vectorial V, se llama sistema generador de V a un conjunto de vectores, pertenecientes a V, a partir del cual se puede generar el espacio vectorial V completo. En este caso, el espacio vectorial V se denomina conjunto generado o espacio generado. [nota 1] Esto también es válido para subconjuntos de V, en esos casos se habla de subconjuntos generados, o.
El Espacio Vectorial R^n Curso de Álgebra Lineal YouTube

Observaciones. La denominación de las dos operaciones no condiciona la definición de espacio vectorial por lo que es habitual encontrar traducciones de obras en las que se utiliza multiplicación para el producto y adición para la suma, usando las distinciones propias de la aritmética.. Para demostrar que un conjunto es un espacio vectorial: . Lo es si sus dos operaciones, por ejemplo.
DETERMINE si el conjunto dado de VECTORES GENERA el espacio VECTORIAL Combinación Lineal YouTube

TUTORÍAS, solución EJERCICIOS, trabajos y SOLUCIONARIOS de libros: https://linktr.ee/el_profe_javiCapítulos0:51 definición conjunto generador de un espacio v.
Espacio vectorial generado YouTube

Motivación para el estudio de los espacios vectoriales. Cuando encontramos varios tipos de matrices en el Capítulo 5, se hizo evidente que un tipo particular de matriz, la matriz diagonal, era mucho más fácil de usar en cálculos.Por ejemplo, si \(A =\left( \begin{array}{cc} 2 & 1 \\ 2 & 3 \\ \end{array} \right)\text{,}\) entonces se \(A^5\) puede encontrar, pero su cómputo es tedioso.
200503 Clase en vivo sobre conjunto de generadores de la imágen de un espacio vectorial YouTube

Concepto y ejercicios del conjunto generador de un espacio vectorial. Definición y ejemplos del elemento genérico de un espacio vectorial.Videos cortos de ál.
AXIOMAS DE UN ESPACIO VECTORIAL Álvarez Lapizco Miguel Ángel 13211477 [PPTX Powerpoint]

Sistema de generadores. Diremos que un conjunto de vectores es un sistema generador del espacio vectorial V, si se puede expresar cualquier vector como la suma del producto de un coeficiente por cada uno de los vectores que forman el sistema de generadores, es decir: